Loops in Python

Overview, Objectives, and Key Terms

In Lecture 5, the basics of programming logic were introduced, including the idea of iteration. The emphasis here and in Lecture 9 is on the logic of iteration and its implementation via while and for loops in Python. To proceed, one must be comfortable with the theoretical coverage of iteration presented in Lecture 5.

Objectives

By the end of this lesson, you should be able to

• Use a while loop to solve simple problems using iteration
• Turn pseudocode and flowcharts into Python code
• Use the graphical debugger in Spyder to trace and debug a program with iteration

Key Terms

• while
• break
• summation problem (as a common loop example)
• numerical convergence (as another common loop example)
• convergence criterion

A Motivating Problem

To jumpstart the lesson, let’s first look back to the example from Lecture 5 in which the elements of an array a are printed. The algorithm, in pseudocode, for solving that task is repeated here:

'''Algorithm to print out the elements of an array'''
Input a and n # where n is the length of array a
Set i to 0
While i < n
    Print a[i]
    Set i = i + 1

We can do that in Python using a nearly identical syntax:

import numpy as np
a = np.array([1, 1, 2, 3, 5, 8, 13])
n = len(a)
i = 0
while i < n:    # always remember the :
    print(a[i]) # indented 4 spaces
    i = i + 1   # also indented 4 spaces

1
1
2
3
5
8
13

Just like the if statement, the while statement requires the pesky : after the condition. Moreover, all the things to be done at each iteration must be underneath and indented to the right of the while.

Here’s a slightly different problem, and one that serves as a template for many other problems: add the integers from 1 through n. An algorithm for solving the problem is shown below.

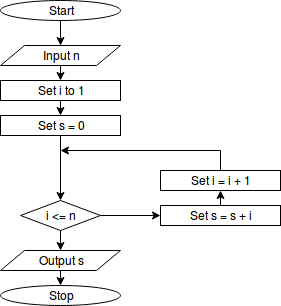
Flowchart for adding integers

This flowchart is very similar to the one we saw earlier for printing the element. The only real addition is the new variable s, short for sum.

Exercise: Explain why using s is better than using sum for representing our integer sum.

We can adapt this flowchart directly to Python:

n = 10 # or we could use input
i = 1
s = 0
while i <= n:
    s = s + i
    i = i + 1
print(s)

55

Is that right? A useful formula for the same sum is \(s = \frac{(n+1)n}{2}\), and substitution of \(n = 10\) does yield \(s = 55\).

Iteration is challenging, for sure. Here are some simple exercises to tackle based on the example above for which you should be able to compute the expected value readily with pen and paper:

Exercise: Write a short program using a while loop to compute the sum of the integers from \(m\) through \(n\). What is the analytical expression for that sum?

Exercise: Write a short program using a while loop to compute the product of the integers from 1 through \(n\). (What is that product called?)

Exercise: Write a short program using a while loop to compute \(a^n\) given a number (int or float) a and an integer n.

The break Clause

So far, iteration has been limited to cases in which a fixed number of iterations is executed, usually with a condition like counter < max_counter. Sometimes, iteration should cease based on criteria that can be satisfied at any value of counter and for reasons unrelated to counter.

As a simple example, suppose we modify the integer summation problem and look instead for the largest value of n that leads to a sum s below some maximum value s_max. You might be tempted to do the following:

s_max = 100
s = 0
i = 0
while s < s_max:
    i = i + 1
    s = s + i
print("i = ", i)
print("s = ", s)

i =  14
s =  105

That’s close, but not quite right: the final value of s is greater then the maximum value of 100. The problem here is that the loop has to repeat until it has produced an s that exceeds the maximum. Thus, in order to terminate, we must already have a value for s greater than we want. A simple fix is a post correction, e.g.,

s_max = 100
s = 0
i = 0
while s < s_max:
    i = i + 1
    s = s + i
s = s - i # subtract off the last amount added
i = i - 1 # and adjust i accordingly
print("i = ", i)
print("s = ", s)

i =  13
s =  91

However, such corrections are not always easy to do. Instead, we can reorganize the while so that it terminates from within the loop. It all starts with the infinite loop:

while True:
    print("this line will be displayed over and over again!")

This loop will never end unless you terminate execution from outside the interpreter. In Spyder, that’s done by pressing the little red square to the upper right of the console. It runs forever because the condition is while True and nothing can ever turn True into False. What we need is some condition within the loop that leads to termination of the iteration. Such conditions can be implemented using the break clause:

while True:
    print("this line will now be displayed just once!")
    break

this line will now be displayed just once!

A break statement may be used anywhere within a while loop. Here, break is executed after just the first iteration. If, instead, we wanted to print the message twice, we could do

counter = 0
while True:
    print("this line will now be displayed just once!")
    counter += 1
    if counter == 2:
        break

this line will now be displayed just once!
this line will now be displayed just once!

Note that an if statement has been inserted within the while statement. Just like if statements can be nested in other if statements, so to can they be nested inside while (and for, and other constructs).

By using the break statement, we can reorganize our program for finding the

s_max = 100
s = 0
i = 0
while True:
    if s + i + 1 > s_max:
        break
    i = i + 1
    s = s + i
print("i = ", i)
print("s = ", s)

i =  13
s =  91

This output is identical to the previous version, and no post-corrections are needed.

Exercise: Run this program in Spyder and use the graphical debugger to trace its execution.

Numerical Convergence

The integer summation problem posed above is one of the canonical examples to use iteration, and it serves as a template for many other tasks. An equally important example is that of numerical convergence.

A very common goal in numerical computing is to produce a sequence of numbers that converges (in the limit of many terms) to some value of interest or, more often, as close to that value of interest as is desired. For example, Taylor series (and similar series) expansions can be used to evaluate the value of mathematical functions near a point of interest. The Taylor series expansion of \(\frac{1}{1-x}\) about \(x=0\) is given by

\[y(x) = \frac{1}{1-x} = 1 + x + x^2 + \sum^{\infty}_{n=3} x^n \, .\]

and for very small \(x\) (\(|x| \ll 1\)), we’d expect just the first few terms of the series to be suffient for approximating \(y(x)\) because \(x^i\) is smaller and smaller for increasing \(i\). The questions, though, are (1) how good is good enough? and (2) when do we know to stop?

The answer to the first question depends on the problem and what sort of information is provided. If the goal is to approximate some quantity, then very rarely is the exact value of that quantity known (otherwise, why would we need the approximation?). For such cases, we can only estimate how good an approximation is.

Exercise: Let \(y(x) = 1/(1-x)\). Approximate \(y(0.1)\) by using the series above, and terminate the iteration when the magnitude of the next term to be added is less than or equal to \(\tau = 10^{-4}\). Print out the approximate value for \(y\), the true value of \(y\), and the number of iterations performed.

Solution:

x = -0.1
y = 1/(1-x) # reference (exact) y
ya = 0 # approximate y
i = 0 # iteration counter
while abs(x**i) > 1e-4:
    ya += x**i
    i += 1
print('approximate value ', ya)
print('  reference value ', y)
print('  # of iterations ', i)

approximate value  0.9091
  reference value  0.9090909090909091
  # of iterations  5

The trick here is to iterate only as long as the next term to be added \(x^i\) is greater then the tolerance \(\tau\). Here, that threshold is \(10^{-4}\). Although the sum of all the terms we’re neglecting could be larger than the tolerance, often the series converges rapidly enough for such a criterion to work well in practice.

Note: A common termination criterion is \(|y_a - y^{old}_a| < \tau\), where \(y_a\) is the current approximation to \(y\), \(y_a^{old}\) is the previous value of \(y_a\), and \(\tau\) is the tolerance.

Sometimes, it’s not easy to pick a suitable tolerance. For some values of \(x\), the program above requires 1000’s of iterations, way more than the 5 observed for \(x=-0.1\). An useful alternative (or additional) termination criterion is to set a maximum number of iterations. By using both, one can provide a program that will produce a solution that meets the tolerance for any case not exceeding the maximum number of iterations allowed.

Note: It is good practice to include a limit on the number of iterations in addition to a tolerance on the approximation.

Based on this discussion, try tackling the following:

Exercise: Explain why we would not want to use while x**i > 1e-4.

Exercise: Modify this program to compute no more than 20 terms of the series. For x = 0.99, which condition causes the loop to terminate? What is the final value of ya?

Exercise: Modify this program to use the absolute error abs(y-ya). Do the results differ? By how much?

This program for approximating \(1/(1+x)\) is a great one for understanding how iteration can be used to solve numerical problems. The same pattern (i.e., keep iterating until the approximation looks good enough) shows up all over the place in the solution of both linear systems (i.e., \(\mathbf{Ax}=\mathbf{b}\)) and nonlinear systems (e.g., finding the roots of \(f(x)\)).

Further Reading

None at this time.