Algorithms, flowcharts, and pseudocode.

Overview, Objectives, and Key Terms

In this lesson, we’ll dive right into the basic logic needed to plan one’s program, significantly extending the process identified in Lesson 2. We’ll examine algorithms for several applications and illustrate solutions using flowcharts and pseudocode. Along the way, we’ll see for the first time the three principal structures in programming logic: sequence, selection, and iteration. Throughout, specialized syntax (Python or otherwise) is avoided (with the exception of the handy slicing syntax introduced in Lesson 3), but variables and simple operators are used.

Objectives

By the end of this lesson, you should be able to

• define what an algorithm is
• decompose problems into a sequence of simple steps
• illustrate those steps graphically using flowcharts
• describe those steps in words using pseudocode

Key Terms

• algorithm
• sequence
• selection
• iteration
• counter variable
• index variable
• condition
• conditional statement
• loop

Algorithms

An algorithm is procedure by which a problem (computational or otherwise) is solved following a certain set of rules. In many computer science departments, entire courses are dedicated to the study of algorithms important for solving a wide variety of problems. Some of the most important algorithms (including a few that we’ll be studying in part throughout the semester) are

• Gaussian elimination (for solving \(\mathbf{Ax}=\mathbf{b}\))
• Bubble sort (for sorting an array of values)
• Quicksort (a better way to sort those same values)
• Sieve of Eratosthenes (for finding prime numbers)
• Babylonian method (for finding square roots)
• Linear search (for finding a value in an array)
• Binary search (a better way for finding that value)
• Dijkstra’s algorithm (for finding, e.g., the shortest path between two cities)
• RSA algorithm (for encrypting and decrypting messages)

Many more such algorithms are listed elsewhere.

It turns out, however, that we apply algorithms all the time in every-day life, often without realizing it. Such occasions might be as boring as choosing one’s outfit for the day based on planned activities, the weather, the general status of laundry (and how many times you think you can wear that pair of jeans), etc. Other occasions of somewhat more importance might include choosing a baby’s name (which might mean making a list, whittling it down, and then convincing your wife that Linus is the one not just because that’s the name of the Finnish-born inventor of Linux). The list goes on and on: life presents problems, and we apply logic to solve those problems.

Sequence by Example: Computing Grades

Let’s consider something with which you are all familiar: a course grading scheme. As a concrete example, suppose the course in question has graded tasks in four categories, each with its own weight:

1. homework - 20%
2. laboratories - 10%
3. quizzes - 10%
4. examinations - 60%

Such a scheme is probably familiar, and you’ve probably used your intuition, knowledge of your grades, and knowledge of this sort of weighting scheme to compute a final percentage. Here, we’ll formalize that process using flowcharts and pseudocode.

To simplify matters somewhat (for now), assume that there are a fixed number of tasks in each category, and each task within a category is worth the same amount. For example, the course might have 5 homework assignments, and each of these assignments might be assessed out of ten points. Take those scores to be 10, 7, 9, 10, and 10.

You might immediately see how the computation of a homework percentage can be broken into several independent steps. For instance, we can first compute the homework score. How? Think carefully. If you were using a calculator, what would you enter? On mine, I can enter 10 followed by a + and then 7 and then another +. After every addition +, it prints out the running total. In other words, it’s automatically storing the running total.

We can be more explicit, though. Before we add any of the scores at all, we can set the total score to zero, and thereafter, we can add each of the homework scores to that total in sequence. When that’s done, we need to compute the total possible score, which is the number of tasks multiplied by the point value per task. Finally, we need to compute the percentage earned on these homework assignments, which is equal to the total homework score divided by the total number of points possible (and then multiplied by 100).

This entire process can be described using pseudocode, which is any informal, high-level (few details) language used to describe a program, algorithm, procedure, or anything else with well-defined steps. There is no official syntax for pseudocode, but usually it is much closer to regular English than computer programming languages like Python. Here is one possible pseudocode representation of the procedure just outlined for computing the homework score:

'''Algorithm for computing homework percentage'''
# Get the inputs needed to compute the homework percentage
Input hw_1_score, hw_2_score, hw_3_score, hw_4_score,
      hw_5_score, number_hw, points_per_hw
# Initialize the total homework score
Set total_score to 0
# Increment the total homework score by each of the homework scores
Increase total_score by hw_1_score
Increase total_score by hw_2_score
Increase total_score by hw_3_score
Increase total_score by hw_4_score
Increase total_score by hw_5_score
# Determine the total number of points possible
Set total_possible to points_per_hw multiplied by number_hw
# Compute the homework percentage
Set hw_percent to 100 times total_score divided by total_possible
# Provide the homework percentage
Output hw_percent

Of course, this might seem long-winded, but it is explicit. As long as the input and output processes are specified (e.g., providing a printout of grades and asking for a final value to be written on that printout), this procedure could be given to most reasonable people and executed without difficulty. For reference, the total homework score (in percent) that one should get from the individual scores above is 92.

Exercise: For each line of the pseudocode above, write the value of total_score, total_possible, and hw_percent. If a variable does not have a value at a particular line, then say it is undefined.

A flowchart of the same procedure is provided below.

Flowchart for Computing Homework Percentage

Now, revisit the bolded word above: sequence. This particular process for computing the homework percentage is a sequence, which is the simplest of the logical structures used in programming. A sequence is nothing more than a set of instructions executed one after another. The number of these instructions and the order in which they are executed is known from the start, just like our example here (and the example seen in Lesson 2).

Selection

The same sort of procedure can be used for all of the grading categories, and hence, let us assume now that we have available the final percentages for homework, laboratories, quizzes, and homeworks. The question now is how to assign a final letter grade based, for example, on the traditional 90/80/70/60 scheme for A/B/C/D. For this grading scheme, anything 90% or higher earns an A, anything less than 90% but greater than or equal to 80% earns a B, and so forth.

Of course, this requires that we first compute the final grade, for which the final percentages and the corresponding category weights are required. In pseudocode, that process can be done via

'''Algorithm for computing final percentage'''
# Get the inputs needed to compute the final percentage
Input hw_percent, lab_percent, quiz_percent, exam_percent,
      hw_weight, lab_weight, quiz_weight, exam_weight
# Initialize the final percentage
Set final_percent to 0
# Increment the final percentage by the weighted contribution from each category
Increase final_percent by hw_percent * hw_weight
Increase final_percent by lab_percent * lab_weight
Increase final_percent by quiz_percent * quiz_weight
Increase final_percent by exam_percent * exam_weight
# Provide the final percentage
Output final_percent

What we need next is to define the grade, and that’s where selection enters the game. Selection refers to a structure that allows certain statements to be executed preferentially based on some condition. Hence, selection is often implemented using conditional statements. In English, a basic conditional statement takes the form If some condition is satisfied, then do something. More complicated statements can be formed, but all conditional statements can be rewritten using one or more of these simple statements.

A basic conditional statement can be represented graphically as shown below.

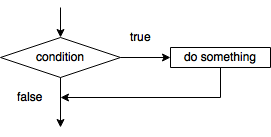
Flowchart fragment for a simple conditional statement

Armed with conditional statements for selection, we can tackle the final grade. Given the final percentage, we check whether that value is greater than 90. If so, the grade assigned is an A. If not, we can further check whether that percentage is greater than or equal to 80 and less than 90. If so, a B. If not, we check against 70 and then 60 for a C and D, respectively. If the percentage has not earned a D by the time we’ve checked, our poor student’s grade, of course, is an F.

This procedure, much like those described previously, can be described compactly in pseudocode:

'''Algorithm to compute the final grade'''
# Get the final percentage
Input final_percent
# Check if the grade is an A
If final_percent >= 90 then
    Set final_grade to A # Indentation helps tie the statement to the condition
# Check if the grade is a B
If final_percent < 90 and final_percent >= 80 then
    Set final_grade to B
# Check if the grade is a C
If final_percent < 80 and final_percent >= 70 then
    Set final_grade to C
# Check if the grade is a B
If final_percent < 70 and final_percent >= 60 then
    Set final_grade to D
# Check if an F
If final_percent < 60 then
    Set final_grade to F
# Provide the final grade
Output final_grade

As a flowchart, this same procedure is shown below.

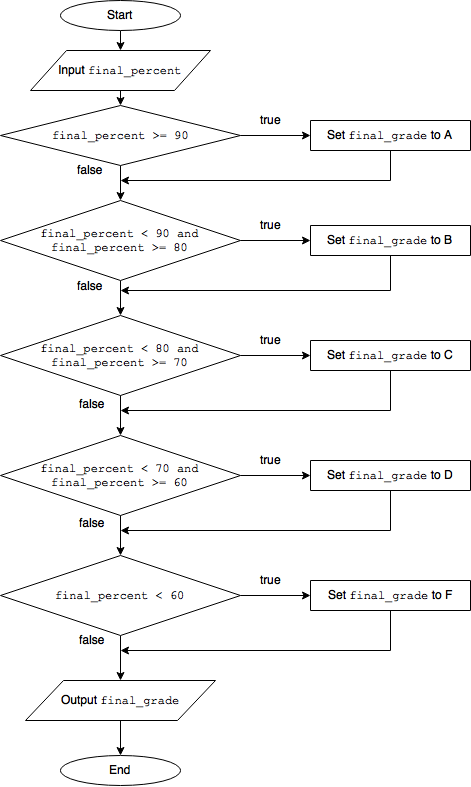
Flowchart for computing the final grade

Iteration

Suppose that the homework grades analyzed above are subjected to a slight policy change: the lowest score is dropped. Such a policy is pretty common. How do we tackle this problem? It requires that we make a decision when adding a particular homework score to the total. In particularly, we skip adding the lowest score.

Exercise: Think back to the scores (i.e., 10, 7, 9, 10, and 10). Now, pick out the lowest score and, importantly, write down how you came to that conclusion. Seriously—think about what you needed to do to choose the lowest number and get it down in words.

When I first glance at the numbers, I see that there are some 10’s and other numbers, and scanning left to right, I pick out 7 as being the lowest of them. Then, keeping track of 7 (subconsciously, in this case), I scan the list and confirm that 7 is, in fact, the lowest score. I’ll bet you do something similar, but computers don’t have eyes (or a subconscience), and we therefore need to define this a bit more carefully.

The Basic Idea

To start, let’s assume that the individual homework grades are stored in an array (e.g., a NumPy ndarray) rather than as separate values. Call this array hw_scores so that we use, e.g., hw_scores[0] and hw_scores[1] instead of hw_1_score and hw_2_score. From this array, we need to pick out which element represents the score to be dropped. Therefore, we need language to describe the process of iterating through the array elements, i.e., iteration. In English, we might say something like “for each score in the array, do something.” More generically, iteration consists of doing that something until some condition is no longer satisfied, as illustrated in the flowchart fragment below:

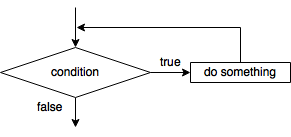
Flowchart fragment for a simple loop

Notice that this flowchart bears a striking similarity to the one shown above for the conditional statement. The difference, however, is that the flow of the program is redirected to before the condition block. In other words, a repeating loop is produced that is broken only if the condition is no longer because of changes made inside the “do something” block. The pseudocode fragment for this same loop is

While the condition is satisfied
  Do something

Let’s apply this to a simple but illustrative problem before moving on to our homework application. Suppose we want to print every value in an array a of length n. A canonical approach to this sort of problem starts by defining an index or counter variable (often named i) that is used to access the ith element of the array during the ith time through the loop. After the ith element has been used, the counter is increased by one, and the loop begins again. Once the counter is equal to the number of elements in the array, the loop is terminated. Here’s the complete algorithm in pseudocode

'''Algorithm to print out the elements of an array'''
Input a and n # where n is the length of array a
Set i to 0
While i < n
    Print a[i]
    Set i = i + 1

and as a flowchart

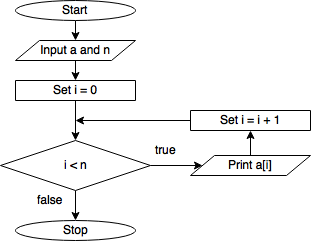
Flowchart for printing the elements of an array

Back to Homework

For our homework example, the condition is “have all the scores been considered?”, while the “something” to be done is checking whether or not a given score is lower than the others. The counter-based approach to iteration developed above can be used to go through each element of the homework score array, thereby ensuring that all the elements are considered. We could compare the ith grade to every other grade (implying an iteration within an iteration), but there is a simpler way. First, we can set the lowest score equal to the first grade (i.e., hw_grades[0]). Then, we can go through all the other scores and compare each to the lowest score. If a score is lower than the current value of lowest score, that score becomes the lowest score. Along the way, we can also keep track of the index (location) of the lowest score within the array. Here’s the idea in pseudocode:

'''Algorithm for finding lowest homework score'''
# Get the homework score array and the number of scores
Input hw_scores, number_hw
# Initialize the lowest score to the first homework score
Set lowest_score to hw_scores[0]
Set lowest_score_index to 0
# Start the counter at 1 since we've already used position 0
Set i to 1
# Begin the iteration
While i < number_hw
    # Update the lowest score if another score is lower
    If lowest_score > hw_scores[i] then
        Set lowest_score to hw_scores[i]
        Set lowest_score_index to i
    # Increment the counter
    Set i to i + 1
# Provide the lowest score and its position in the array
Output lowest_score, lowest_score_index

Here it is also as a flow chart:

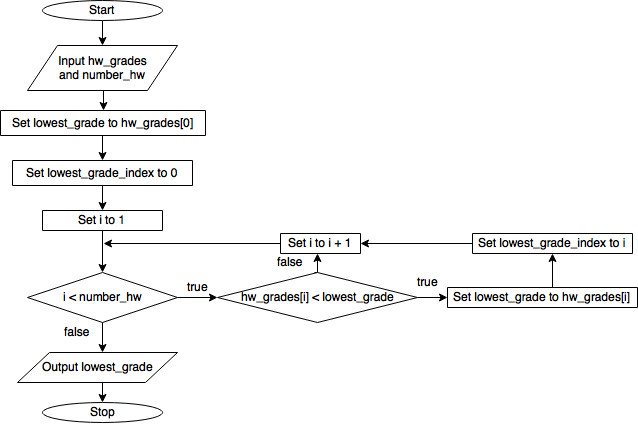
Flowchart for finding the lowest grade

Putting It All Together

By now, we have all the pieces needed to compute the total homework percentage when the lowest score is dropped. Here it is, all together, in pseudocode:

'''Algorithm for computing homework percentage when lowest grade is dropped'''
# Get the inputs needed to compute the homework percentage
Input hw_scores, number_hw, points_per_hw
# Initialize the lowest score to the first homework score
Set lowest_score to hw_scores[0]
Set lowest_score_index to 0
# Start the counter at 1 since we've already used position 0
Set i to 1
# Begin the iteration
While i < number_hw
    # Update the lowest score if another score is lower
    If lowest_score > hw_scores[i] then
        Set lowest_score to hw_scores[i]
        Set lowest_score_index to i
    # Increment the counter
    Set i to i + 1
# Initialize the total homework score
Set total_score to 0
# Reset the counter to zero
Set i to 0
# Begin the loop over all homeworks
While i < number_hw
    # Add any score that is not the lowest score
    If i is not equal to lowest_score_index then
       Set total_score to total_score + hw_scores[i]
    # Increment the counter
    Set i to i + 1
# Determine the total number of points possible.  Note
# that the number of homeworks is reduced by one to
# account for the drop.
Set total_possible to points_per_hw * (number_hw - 1)
# Compute the homework percentage
Set hw_percent to 100 * total_score / total_possible
# Provide the homework percentage
Output hw_percent

**Exercise**: Create a flowchart for this algorithm.

Practice Problems

Planning out the logic needed to solve problems can be tricky, and most students require lots of practice. Each of the topics discussed above will be the focus of the next several lessons as we dive into their implementation in Python. However, now is the time to start applying the sequence, selection, and iteration constructs, and listed below are several great practice problems to help get you started.

Develop an algorithm for each of the following tasks using both pseudocode and a flowchart. Note, many of these tasks represent great practice problems for Python programs, too. Of course, if you plan out the logic first using the tools employed in this lesson, the implementation of your solution in Python later on should be much easier!

• Prepare a pot of coffee.
• Prepare a cup of coffee for your friend. (Cream or sugar?)
• String a guitar.
• Choose your outfit (making sure to account for the day of the week and the weather).
• Determine the largest number in an array.
• Determine the second largest number in an array.
• Determine whether an integer is even.
• Determine whether an integer is prime.
• Determine whether a given year is a leap year.
• Determine the next leap year after a given year.
• Divide one number by another number using long division
• Determine the sum of an array of numbers.
• Determine the sum of the elements of an array of numbers that are divisible by 3 and 5.
• Given any two integers n and d, determine whether the quotient n/d leads to a finite decimal number (e.g., \(5/4 = 1.25\)) or an infinite decimal number (e.g., \(1/3 = 0.3333\ldots = 0.\bar{3}\)).
• Extend the homework grade algorithm to drop the two lowest scores.
• Determine a final grade in ME 400 following the course grading policies (including drops).

Further Reading

Here is a nice example of flow chart construction for the game of hangman.